Why another description about the circle of fifths you might ask. After researching dozens of articles and videos about the circle of fifths, I wanted to present the information a little bit differently and combine good ideas I found, so that it gives more insight and makes it easier for the learner.
If you already know about the circle of fifths (its definition and how it is constructed and used) you can skip the first two chapters.
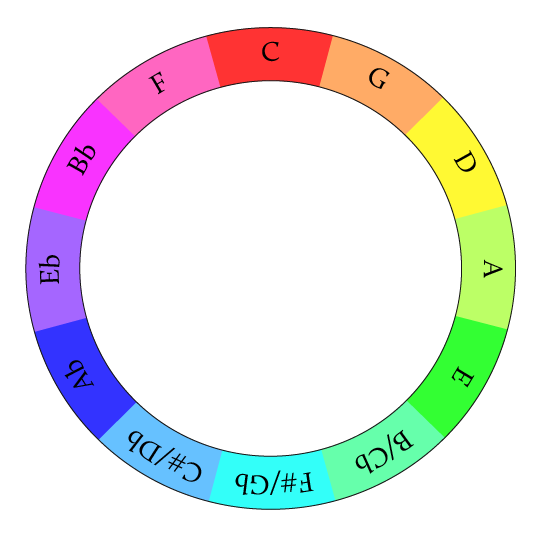
The Circle of Fifths is a fundamental concept in music theory that serves as a visual guide to the relationships among the 12 tones of the chromatic scale, their key signatures and their corresponding modes.
It organizes these elements in a circular layout where each key is a perfect fifth higher than the preceding one as you move clockwise. A perfect fifth is a musical interval that spans five notes in a major scale, creating a harmonious and stable sound.
The Circle of Fifths helps musicians understand the structure of music by revealing how keys are related to one another, facilitating easier key changes, and highlighting the interconnectedness of scales and chords.
As a practical tool, the Circle of Fifths enhances a musician's ability to improvise, compose, and grasp harmonic relationships, making it essential for those looking to deepen their musical knowledge and skills.
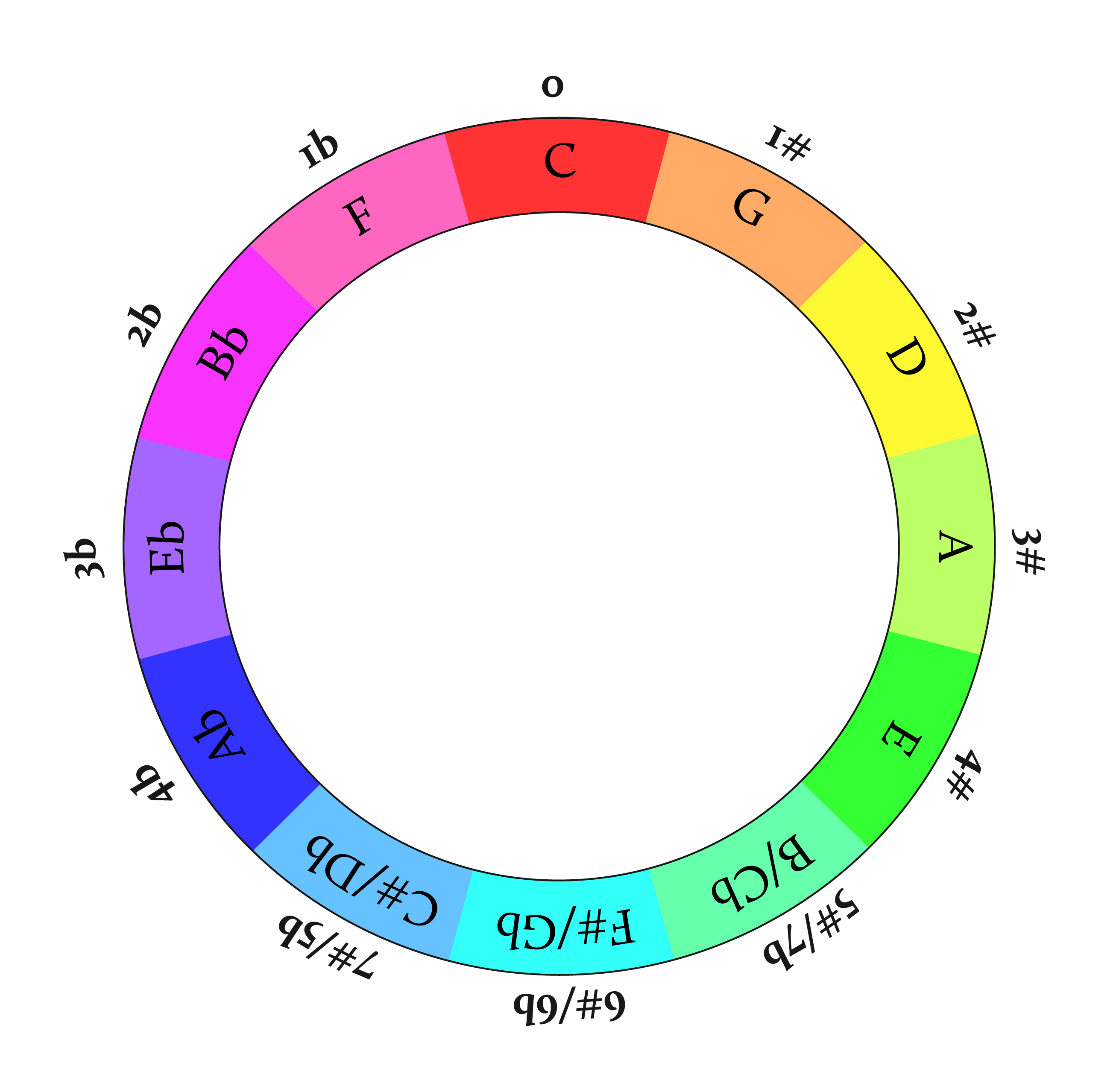
The Circle of Fifths is constructed by arranging the 12 notes of the chromatic scale into a circle, where each step from one note to the next is an interval of a perfect fifth. Here's a step-by-step explanation of how it is constructed:
Start with a Note: You begin with any note; commonly, C is used as the starting point.
Move Up a Perfect Fifth: From C, go up a perfect fifth to G. This is done by counting up seven semitones (or half steps) from C. You can also think of it as an interval spanning five consecutive notes in a diatonic scale or a pair of pitches with a frequency ratio of 3:2.
Continue the Pattern: From G, move up another perfect fifth to D. Repeat this process, each time moving up a perfect fifth from the last note.
Complete the Circle: Continue this pattern until you return to the starting note. The sequence you follow from C would be C, G, D, A, E, B/C♭, F#/G♭, C#/D♭, A♭, E♭, B♭, and back to C. This forms a circle.
Flats and Sharps: If you go clockwise you add a sharp at every step, and if you go counterclockwise you add a flat at every step.
The concepts of "relative" and "parallel" modes refer to different ways of understanding and comparing modes that share certain relationships with each other, particularly in how they relate to major and minor scales. We will start by explaining the 'relative modes' and then move to the 'parallel modes'.
The modes of the major scale are built by starting the scale on different notes within the scale, but using the same set of pitches. Each mode has a unique starting point and thus a distinct sound or flavor. Here's how each mode is built from the major scale:
Ionian: This is the major scale itself, starting on the first degree. For example, C Ionian is C-D-E-F-G-A-B-C.
Dorian: Start on the second degree of the major scale and continue to the same note an octave higher. For example, if you start on D in the C major scale, the D Dorian mode is D-E-F-G-A-B-C-D.
Phrygian: Start on the third degree of the major scale. For instance, E Phrygian, using the C major scale notes, would be E-F-G-A-B-C-D-E.
Lydian: Begin on the fourth degree of the major scale. Using C major again, F Lydian would be F-G-A-B-C-D-E-F.
Mixolydian: Start on the fifth degree. In C major, G Mixolydian would be G-A-B-C-D-E-F-G.
Aeolian: This mode is also known as the natural minor scale, starting on the sixth degree. In C major, A Aeolian is A-B-C-D-E-F-G-A.
Locrian: Start on the seventh degree. B Locrian, using the C major scale, would be B-C-D-E-F-G-A-B.
Each mode has a distinctive set of intervals that gives it a unique character. These different starting points alter the pattern of whole and half steps, which changes the emotional and harmonic content of the music. This is why modes are widely used in various music genres to create different moods and textures.
Relative modes are different modes that share the same key signature but start on different notes of the scale. They contain the same pitches but are arranged in a different order, starting from a different root note.
Example: C major (Ionian mode) and A minor (Aeolian mode) are relative to each other. Both share the same key signature (no sharps or flats) but start on different notes. If you play all the white keys on a piano from C to C, you get C major; if you play from A to A, you get A minor.
Parallel modes, on the other hand, begin on the same root note but have different key signatures. This means they alter some of the pitches by using sharps or flats to achieve different modal sounds.
Instead of using the circle of fifths to dial in the mode you want, you can also construct the modes by sharpening or flattening different scale degrees.
Lydian is the brighest mode, you add a sharpened 4 to the major scale to construct it. Ionian is simply the major scale (which is our starting point, so there is no need to sharpen or flatten any degrees). The rest of the modes add flats and the more flats you add, the 'darker' the mode.
For Mixolydian you flatten the 7, for Dorian the 7 and 3, for Aeolian the 7, 3 and 6, for Phrygian the 7, 3, 6 and 2 and for Locrian the 7, 3, 6, 2 and 5.
| Mode |
Scale Degrees |
|---|
| Lydian |
1 2 3 #4 5 6 7 |
| Ionian |
1 2 3 4 5 6 7 |
| Mixolydian |
1 2 3 4 5 6 ♭7 |
| Dorian |
1 2 ♭3 4 5 6 ♭7 |
| Aeolian |
1 2 ♭3 4 5 ♭6 ♭7 |
| Phrygian |
1 ♭2 ♭3 4 5 ♭6 ♭7 |
| Locrian |
1 ♭2 ♭3 4 ♭5 ♭6 ♭7 |
Example: C major and C minor are parallel. Both start on C, but C major uses the notes C-D-E-F-G-A-B, while C minor (typically referring to the natural minor, or Aeolian mode) uses the notes C-D-E♭-F-G-A♭-B♭. Here, E, A, and B are flattened compared to their pitches in C major.
Understanding these relationships can be very useful in composition and improvisation, as it allows a musician to shift the mood or color of the music by changing modes while retaining a common tonal center or maintaining the same melodic content but altering its harmonic context.
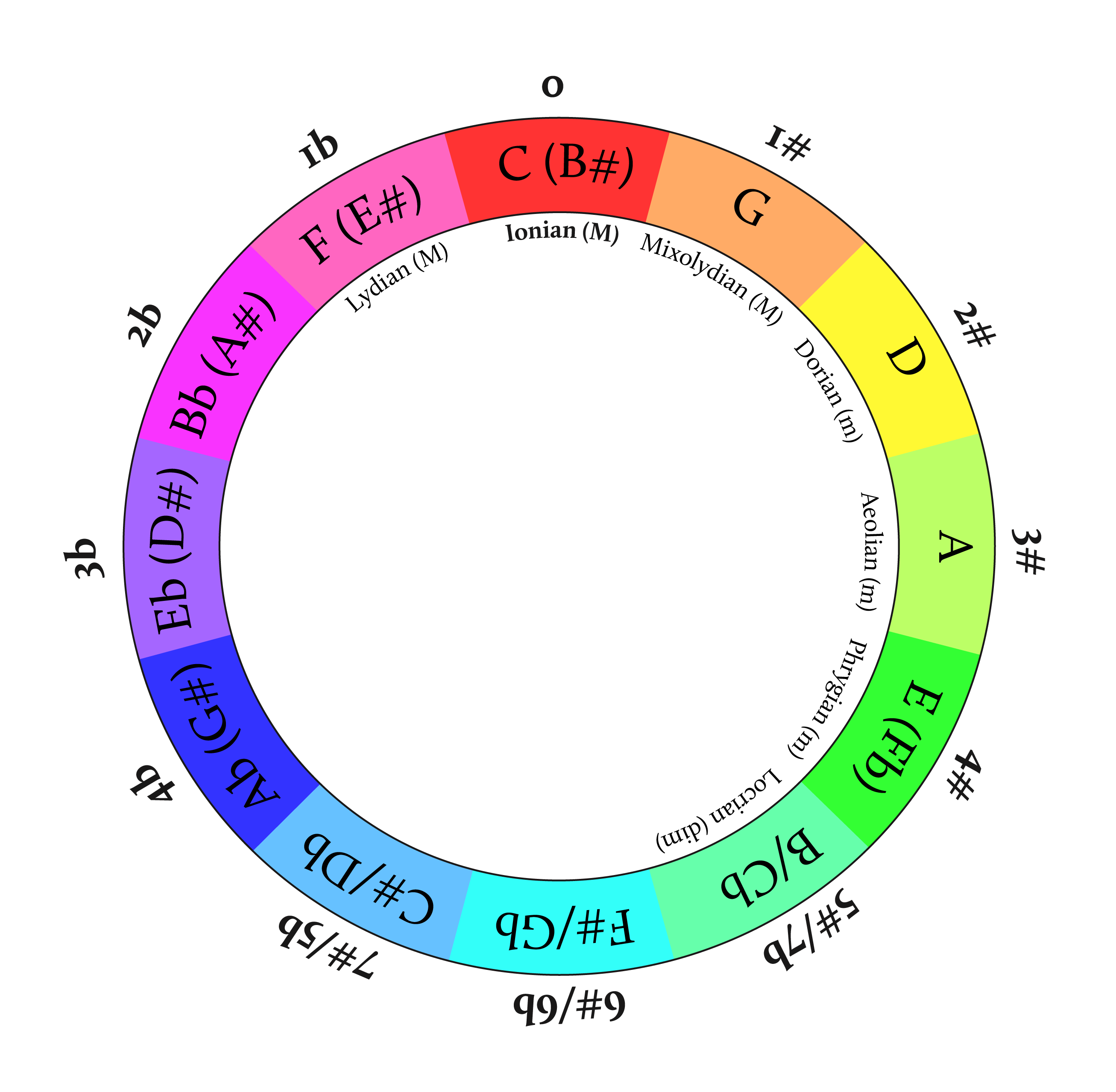
The representation of the circle of fifths you find on this page is a little bit different to the one you encounter most frequently. First it gives you all the notes of the different scales directly, without having to memorize the order of sharps (e.g. Father Charles Goes Down And Ends Battle) and flats (i.e. Battle Ends And Down Goes Charles' Father),
as you can read them from the inner circle (the notes relative to one of the modes form part of your scale).
The inner circle is rotatable, so you can turn it to dial in the modes you want. The sharps and flats are those relative to the corresponding ionian mode.
The circle also easily shows all the modes without having to memorize the order of their relative brightness (from brightest to darkest: Lydian, Ionian, Mixolydian, Dorian, Aeolian, Phrygian, Locrian).
Example: Suppose you're looking for Bb Dorian, so you rotate the inner circle so that Dorian is aligned with Bb. You immediately see that the notes in this mode are: Db, Ab, Eb, Bb, F, C and G and the relative modes starting on these different notes (e.g. Db Lydian, F Aeolian, etc.).
You can also read that there are 4 flats in this mode by looking at Ionian and looking at the outer circle with the number of sharps and flats.
My work on the Circle of Fifths as well as this document are released under the ‘Creative Commons Attribution-NonCommercial 4.0 International (CC BY-NC 4.0)’ licence.
July 2024
