if a colour is fully saturated, it cannot be very light or very dark.
Colour is most commonly defined by its hue, saturation and lightness (often called HSL in image editing software). This vision of colour is quite intuitive: the hues are laid out in a circle and we can vary the lightness and saturation for every one of these hues. The entire colour space is thus represented in a bicone.
To better understand how this works, we can cut out a triangle for any given hue from this bicone. In the example below, we have a triangle for a magenta-like hue, but we could construct such triangles for any hue in the colour circle.
By construction, the hue is fixed in this triangle, but we can vary lightness and saturation.
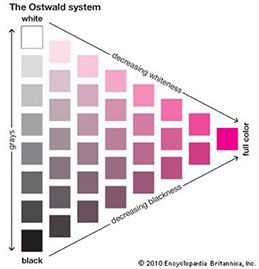
The lightness varies from the bottom to the top (from black to white) and the saturation increases from the left (where the colour is grey) to the right (where the colour is fully saturated).
This colour triangle was already used by Wilhelm Ostwald, Nobel prize winner and one of the leading figures of the Ido language (more on this probably later on Steve Walesch Analytics) in his colour model in 1916. His Ostwald Colour System was influenced by work of Albert Henry Munsell and in turn influenced many others.
Unfortunately, saturation and lightness are usually not constrained in these sliders: you can configure any saturation you like with maximum lightness, leading to white (or similarly with minimum lightness, leading to black).
I wanted to create a similar system, that keeps the basic elements of the HSL model, but that incorporates constraints:
This is obvious by looking at the colour triangles and the bicone.
So I started to define all RGB colours by their respective parts of white, black and chroma. The resulting triplet (whiteness, blackness and chromaticness) always sums to exactly one, expressing the fact that all tints, tones and shades can be constructed by mixing white, black and the respective ‘pure colour’. This closely resembles the colour triangle in the Ostwald model as each point defined by this approach lies within the colour triangle for the respective hue.
The whiteness, blackness and chromaticness triplet is at the basis of my constrained HSL model. The hues are derived in the same way as in the traditional HSL model. The saturation is simply the percentage of ‘pure colour’ in the colour mix. The lightness is the percentage of white + 1/2 of the percentage of ‘pure colour’. This is explained by the fact that all fully saturated colours lie on the same plane as medium grey (RGB 128, 128, 128) and that medium grey is exactly half the lightness of white.
We can thus also put simple constraints on minimum and maximum lightness with respect to saturation:
This leads to the following rules:
I implemented this constrained HSL model in the interactive Jupyter notebook (see below).
The second contribution I wanted to make, was to devise a colour naming system. I found that most colour naming systems were either too simplistic (having a very limited number of different colours), overly complicated or unstructured. The NCS system (which is great for many professional use cases) for instance uses a cryptic system, where ‘2050Y90R’ is a valid colour name. This is overly complicated for everyday use by lay people. Also, the HTML colour names are unstructured, leading to a large vocabulary of sometimes puzzling colour names: how many people know what the colours Gainsboro, Wisteria and Zinnwaldite look like?
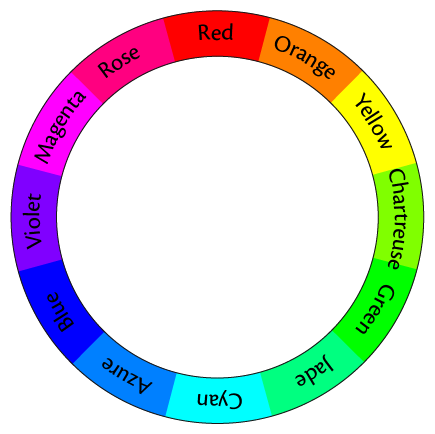Why not use qualifiers of saturation and lightness, that most people can easily relate to and combine them with some commonly used names for hues? In my system, I chose to name the primary colours red, green and blue, the secondary colours yellow, cyan and magenta and the following tertiary colours: orange (30° on the colour wheel), chartreuse (90°), jade (150°), azure (210°), violet (270°) and rose (330°).
Quaternary colours have no specific names but are composed with the names of the two tertiary colours that are closest to it (e.g. 285° is named ‘violet-magenta’.
The lightness of a colour gives it the following qualifiers:
A similar system exists for saturation:
Note that because of the constraints we spoke about earlier, some combinations do not exist: we cannot have a ‘vivid and very light red’ for example.
Two examples of colour names in the Walesch Colour Naming System could be ‘saturated light violet’ and ‘desaturated and very dark orange-yellow’.
A special case is when saturation is equal to 0: when lightness is 0, the colour is named ‘black’, when lightness is 1, the colour is named ‘white’. The intermediate lightness levels follow the same logic as for colours with non-zero saturation: very dark grey, dark grey, medium grey, light grey and very light grey.
The interactive app here below, allows you to use RGB sliders and get the corresponding whiteness-blackness-chromaticness triplets, the constrained-HSL values, a colour preview and the name of the colour in the Walesch Colour Naming System.
You can also use the sliders of my constrained HSL model and get the RGB values, the colour preview and the name of the colour in the Walesch Colour Naming System.
You can also download an interactive Python version of the app as a download (Jupyter notebook).
I also think that there are many excellent colour systems out there that cover different use-cases for colour, like the NCS system or the HCL system (very useful for qualitative colour ramps for example). Maybe my constrained HSL model and the Walesch Colour Naming System will find their use cases too.
I encourage you for feedback that will allow this project to improve.
My work on the whiteness-brightness-colourfulness, the constrained HSL model, the Walesch Colour Naming System as well as this document and the interactive Jupyter notebook are released under the ‘Creative Commons Attribution-NonCommercial 4.0 International (CC BY-NC 4.0)’ licence.
November 2017